【基本情報技術者試験】算術シフトについて学ぼう

本記事では基本情報技術者試験にも出題される論理シフトについて解説しています。目次は以下の通りです。

シフト演算とは

前提としてコンピュータ上では厳密には加算演算しかできないです。
ただ、現実としてかけ算や割り算をコンピュータ上で行いたいですよね。
そこで登場するのがシフト演算です。シフト演算は左右のビットをずらすことにより乗除の演算をすることをいいます。シフト演算には論理シフトと算術シフトがあります。
本記事では算術シフトにフォーカスして説明します。

算術シフト

算術シフトは符号について考えるシフト演算です。
ようはマイナスの数も対応できるよっていうシフト演算ですね。符号ビットをつけるだけで違うのかよっといわれそうですが、シフト演算の操作方法は変わっていきます。
算術シフトには算術左シフトと算術右シフトの2種類があります。操作方法は以下で確認しましょう。

算術左シフト

算術左シフトは整数のかけ算を算術シフトで表すものです。
具体例を以下に示します。

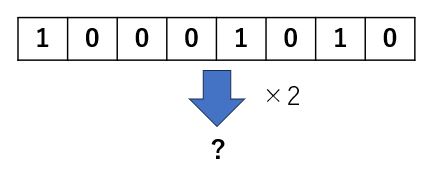
\( 10001010_{(2)} \)を2倍すると仮定します。
ちなみに1番先頭が符号ビットで、-を表しています。
一回10進法に直す方法で行うと、
$$ -1010_{(2)}=-(2^3+2)=-10_{(10)} $$
$$ -10\times 2=-20 $$
$$ -20_{(10)}= -10100_{(2)}$$
となります。
今回便宜上2進法の前に符号をつけています。一方で左シフトを用います。2倍は2の1乗なので、左に1ビット分シフトすればいいのです。そうすると次のようになります。

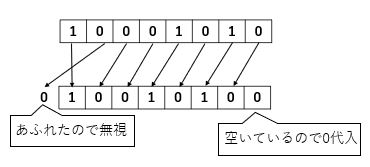
よって、答えが\( 10010100_{(2)} \)となり、10進法に直したときと同じようになります。
ちなみに4倍だと2の2乗なので、左に2つ、8倍だと2の3乗なので、左に3つシフトすることができます。

算術右シフト

算術右シフトは整数の割り算を算術シフトで表すものです。なので、左シフトと逆のパターンですね。具体例を以下に示します。

\( 10001010_{(2)} \)を2で割る、すなわち\( \frac{1}{2} \)倍すると仮定します。
一回10進法に直す方法で行うと、
$$ -1010_{(2)}=-(2^3+2)=-10_{(10)} $$
$$ -10\times\frac{1}{2}=-5 $$
$$ -5_{(10)}= -101_{(2)}$$
となります。
一方で右シフトを用います。\( \frac{1}{2} \)倍は\( \frac{1}{2} \)の1乗なので、右に1ビット分シフトすればいいのです。
そうすると次のようになります。

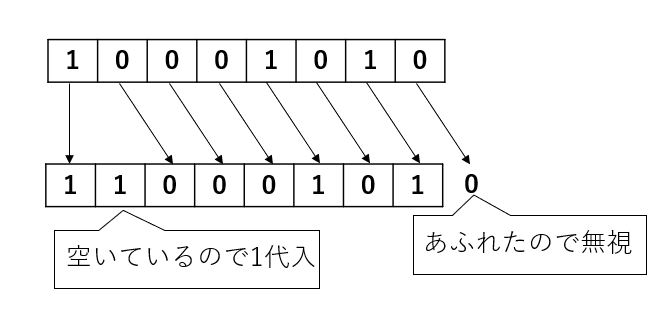
よって、答えが\( 11000101_{(2)} \)となり、10進法に直したときと同じようになります。ここで注意なのが、ちなみに\( \frac{1}{4} \)倍だと\( \frac{1}{2}\)の2乗なので、右に2つ、\( \frac{1}{8} \)倍だと\( \frac{1}{2} \)の3乗なので、右に3つシフトすることができます。

まとめ

本記事のポイントを以下にまとめます。