本記事では基本情報技術者試験にも出題される論理演算の性質について解説しています。
目次は以下の通りです。
論理演算とは
論理演算は真と偽の2つの値を用いて行われる演算で、演算の結果も真または偽となります。コンピュータ上では2進数を扱うため、真は1を、偽は0を表します。
論理演算の性質
論理演算の性質は基本的には四則演算と似たようなイメージでいいでしょう。たくさんあるのでどんどん紹介していきます。
基本法則
基本法則は法則というより定義に近いものや以下の法則に該当しないものを指すと考えてくれればいいと思います。
式的には以下のような形です。
$$ 0+A=A\\
1+A=1\\
A+\bar{A}=1\\
0\cdot A=0\\
1\cdot A=A\\
A\cdot \bar{A}=0\\
\bar{\bar{A}}=A$$
なぜ成り立つかはベン図や真理値表を用いればわかると思います。
たとえば、\( A+\bar{A}=1\)に関してベン図に描くと次の通りです。
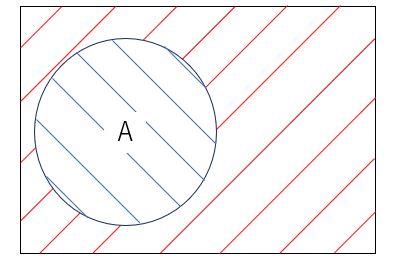
ただし、\(A \)は青の斜線、\(\bar{A} \)は赤の斜線で示しています。+は論理和なので、足し算すると全体を表します。
また、\(A\cdot \bar{A}=0 \)に関して真理値表を用いると次の通りです。
| \(A \) | \(\bar{A} \) | \(A\cdot \bar{A}=0 \) |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
・は論理積なのでどちらに0があれば0確定なので、\(A\cdot \bar{A}=0 \)となります。
このようにベン図をや真理値表を用いれば上の性質がすんなり入ってきます。なので、覚える重要性はそこまで高くないです。
交換則
交換則は足し算やかけ算の順番を逆にしても等しいという法則です。こちらは四則演算と同じ形でできます。
式的には次のようになります。
$$ A+B=B+A\\
A\cdot B=B\cdot A
$$
結合則
結合則は足し算やかけ算にかかるかっこはどこにおいても等しいという法則です。こちらは四則演算と同じ形でできます。
式的には次のようになります。
$$ A+(B+C)=(A+B)+C\\
A\cdot (B\cdot C)=(A\cdot B)\cdot C$$
分配則
分配則は、加法と乗法の間で成り立つ法則です。こちらは四則演算と同じ形でできます。
式的には次のようになります。
$$ A\cdot (B+C)=A\cdot B+A\cdot C $$
吸収則
吸収則はある値とその値と何かを論理和や論理積したものは、元の値と等しくなる法則です。
式的には次のようになります。
$$ A+(A\cdot B)=A\\
A\cdot (A+B)=A$$
べき等則
べき等則はある値とその自身を論理和や論理積した場合には、元の値と等しくなる法則です。
式的には次のようになります。
$$ A+A=A\\ A\cdot A=A$$
ド・モルガンの法則
こちらの法則は試験に出やすい法則の一つです。ド・モルガンの法則は、論理和と論理積における否定を変換する法則で、論理式内の否定を分配してANDやORの関係を変えます。つまり、否定を分配することで等価な式を得られます。この法則は論理和、論理積、そして否定の間で成り立つ規則性です。
式で書くと下のようになります。
$$ \overline{A\cdot B}=\bar{A}+\bar{B}\\
\overline{A+B}=\bar{A}\cdot\bar{B} $$
抑えておくべきか・の否定は+であり、+の否定は・である点です。
まとめ
本記事のポイントを以下にまとめます。
・交換則、結合則、分配則は四則演算とほぼ同一
・そのほかの演算はベン図や真理値表を用いれば成り立つ理由が確認できる
・ド・モルガンの法則は、論理和と論理積における否定を変換する法則
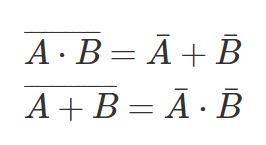

コメント