【基本情報技術者試験】2分木

本記事では基本情報技術者試験にも出題される2分木について解説しています。目次は以下の通りです。

そもそも木構造とは

木構造は階層構造を持つデータ形式で、節と枝から成り立ち、根から始まり葉で終わります。節同士は親子関係で、親が上で子が下に位置します。木構造でも代表的な2分木について説明します。

2分木とは

2分木は各枝の分岐が2つ以下であり、親が最大2つの子を持つ木の一種です。図で表すと次の通りです。

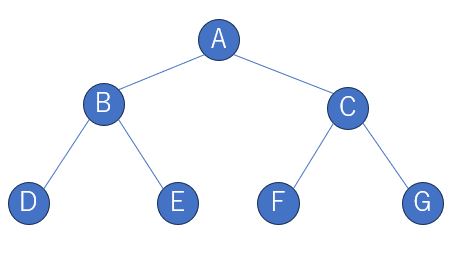
2分木の具体例として以下の3つがあります。
・完全2分木
・2分探索木
・ヒープ

完全2分木

完全2分木は、根から葉までの深さがすべて等しい木構造です。通常は深さが同じですが、1番左に深い葉があり、木全体が左詰めになっている場合も、特例として完全2分木に含まれます。下のような図になります。

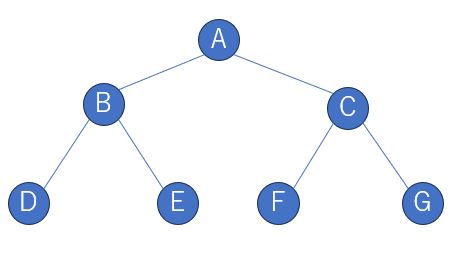
2分探索木

2分探索木は、各節が左の子より小さく、右の子より大きい値を持つ木構造です。この特性により、探索や挿入といった操作が平均的に効率的に行えます。左側の子供は親よりも小さく、右側の子供は親よりも大きな値を持つ規則性を持ち、全ての節において「左側の子の値<節の値<右側の子の値」という大小関係を保ちます。なので節には番号が割り振られており、具体的には以下のようになります。

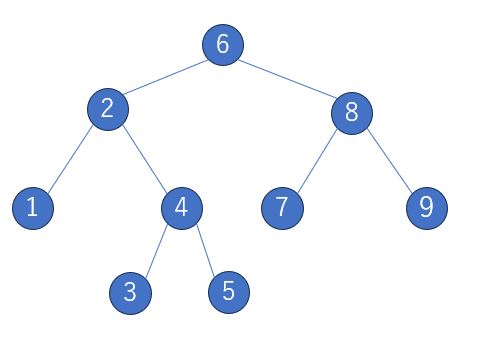
例えば3を探索したい場合は次のようなステップになります。

ステップ1:根の6と比較します。
3<6なので、左側の節に進みます。
ステップ2:節の2と比較します。
2<3なので、右側の節に進みます。
ステップ3:節の4と比較します。
3<4なので、左側の節に進みます。
ステップ4:節の3と比較します。
3=3なので探索終了となります。

ヒープ

ヒープは節ごとに親の値が子より小さいかまたは大きいかを持つ木構造です。親が子より小さい場合根は最小値を持ち、親が子より大きい場合は最大値を持ちます。なので節には番号が割り振られており、具体的には以下のようになります。

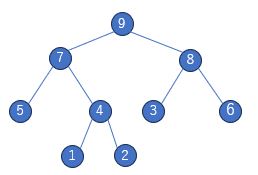
これは根が最大値のときを表しています。

まとめ

本記事のポイントを以下にまとめます。