本記事では基本情報技術者の小数の基数変換について解説しています。
目次は以下の通りです。
10進法から2進法の変換
簡潔に言うと、「2をかけつづける」という感じです。
具体的なステップは以下のような感じです。
ステップ
1.小数に2をかけます。
2.整数部分と小数部分にわけます。
3.小数部分に2をかけます。
4.整数部分と小数部分にわけます。
5.3~4を繰り返します。
6.「小数部分が0になったとき」or「整数部分が周期的に変化した段階」で終了します。
7.あとは整数部分を並べるだけです。
2進法だと2をかけますが、n進法だとnを書ければ大丈夫です。
例題
2問ほど示します。
1.(0.375)を2進法で示せ
2.(0.6)を2進法で示せ
解説
1.
0.375×2=0.75
0.75×2=1.5
0.5×2=1.0
小数部分が0になったので終了します。
あとは整数部分を並べると答えは0.011になります。
2.
0.6×2=1.2
0.2×2=0.4
0.4×2=0.8
0.8×2=1.6
0.6×2=1.2
0.2×2=0.4
0.4×2=0.8
0.8×2=1.6
このように整数部分を見ると1001という風に周期的に変化しています。ゆえに、0.1001が答えになります。
2進法から10進法の変換
こちらは逆に小数第i位の数値に対して1/2のi乗を掛ければよろしいです。なので、整数のときとやり方をほぼ本質的には変わりません。
なのでこちら公式でかきます。
$$ 0.abc…→\frac{1}{2}a+\frac{1}{2^2}b+\frac{1}{2^3}c+… $$
2進法だと2をかけますが、n進法だとnにすれば大丈夫です。
例題
0.101を10進法で示せ
解説
$$ 0.101\\ →1\times\frac{1}{2}+0\times\frac{1}{2^2}+1\times\frac{1}{2^3}\\=\frac{5}{8}=0.625 $$
練習問題
練習問題として3問出題します。
1.(0.75)を2進法で示せ
2.(0.4)を2進法で示せ
3.(0.1101)を10進法で示せ
解説
1.
0.75×2=1.5
0.5×2=1.0
小数部分が0になったので終了します。
あとは整数部分を並べると答えは0.11になります。
2.
0.4×2=0.8
0.8×2=1.6
0.6×2=1.2
0.2×2=0.4
0.4×2=0.8
0.8×2=1.6
0.6×2=1.2
0.2×2=0.4
このように整数部分を見ると0110という風に周期的に変化しています。ゆえに、0.0110が答えになります。
3.
$$ 0.1101
\\ →1\times\frac{1}{2}+1\times\frac{1}{2^2}+0\times\frac{1}{2^3}+1\times\frac{1}{2^4}\\ =\frac{13}{16}=0.8125 $$
まとめ
本記事では小数の基数変換について学びました。10進法から2進法への変換は、2をかけ続ける操作を用いて行います。2進法から10進法への変換は、各ビットの位置に対応する1/2のべき乗を考慮し、小数第i位の数値に1/2のi乗を掛けることで行います。
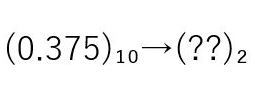


コメント