【深層学習】勾配降下法について学ぼう

本記事では勾配降下法について解説しています。目次は以下の通りです。

勾配降下法とは

勾配降下法は数学的に用いられる最適化の手法であり、Gradient Descentと英語で呼ばれます。損失関数の勾配に沿って、損失関数が最小になる点を探索するアルゴリズムです。そして、この際に重みの値を更新する必要があり、重みの更新の進捗を表す変数として学習率があります。ちなみに学習率は別名ハイパーパラメータとも呼ばれます。
まとめると、重みを変化させることにより損失関数の最小値を見つけ、
損失関数が最小になった重みを求めるという形です。
この勾配降下法にも種類があるので、軽く紹介していきます。

最急降下法

上の定義のものが最急降下法で、式としては次のようになります。
$$ w_{t+1}=w_t-\alpha \bigg(\frac{\partial L}{\partial w} \bigg) $$

この方法を懸念としては一言でいうと最小値ではなく、極値になってしまう可能性があることです。
具体的には次の損失関数のグラフに示します。

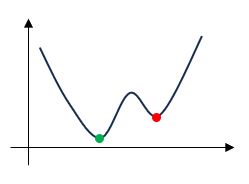
図のように右側から始めると学習率によっては、赤い点である極値で学習が終わる可能性があります。余談ですが、極値や最小値は数学ワードなので、情報系でいうと極値のことを局所最適解、本当の最小値のことを大域最適解と呼びます。

確率的勾配降下法

こちらはSGDとも呼ばれますね。確率的勾配降下法は一部のデータセットを用いて行います。それにより、計算コスト削減につながります。
ただ、学習中の振動により収束が遅くなるデメリットもあります。

モメンタム

こちらは学習率が二つあるのが特徴です。式的には次のように書けます。
$$ v_{t+1}=\beta v_t+(1-\beta)\bigg(\frac{\partial L}{\partial w}\bigg)\\
w_{t+1}=w_t-\alpha v_{t+1} $$

ここでの\(\alpha\)と\(\beta\)が学習率になります。

まとめ

本記事のポイントを以下にまとめます。