【深層学習】活性化関数を知ろう

本記事では活性化関数について解説しています。目次は以下の通りです。

活性化関数とは

活性化関数はニューロンの入力数値を変換して次のニューロンへの出力を生成する関数です。特徴としては非線形関数である点と微分可能である点です。代表的な活性化関数を列挙していきます。
それぞれの特徴をしっかり押さえましょう。

ステップ関数

以下のような式で定義できます。

$$ f(x)=\left\{ \,
\begin{aligned}
& 1 = (x>a) \\
& 0 = (x\leq a)
\end{aligned}
\right . $$

上の式の\( a \)が0なのが一般的です。階段関数とも呼ばれ、0か1が出力されます。関数の勾配(傾き)が0なのも特徴です。

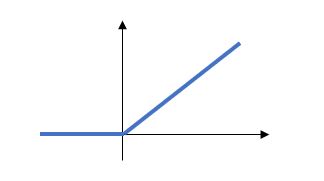
ReLU関数

以下のような式で定義できます。
$$ f(x)=\left\{ \,
\begin{aligned}
& x = (x>a) \\
& 0 = (x\leq a)
\end{aligned}
\right. $$

ランプ関数とも呼ばれ、隠れ層にて高い性能で最適化ができるのが特徴です。また、勾配消失が起きにくいのも利点として挙げられます。

シグモイド関数

以下のような式で定義できます。
$$ f(x)=\frac{1}{1+e^{-ax}} $$

2つに分類する問題にも使用され、範囲は\( 0\leq f(x)\leq 1\)です。ステップ関数と違い、傾きが\(x\)の値により変わります。
また勾配消失問題が起こるため、隠れ層への適応が難しいです。

tanh関数

以下のような式で定義できます。
$$ f(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}} $$

シグモイド関数と概形は似ていますが、範囲が範囲は\(-1\leq f(x)\leq 1\)という違いがあります。なので、関数の性質としてはシグモイド関数に似ています。

まとめ

本記事のポイントを以下にまとめます。