本記事では行列の基本について解説しています。目次は以下の通りです。
線形代数とは
まず、線形代数という学問について説明します。
線形代数とは数学の学問の一つで、線形空間や線形変換について考える分野です。範囲として高校から大学までの内容になります。なお、こちらを学ぶにはある程度の高校数学の知識が必要となるが、わかるように記していきますので、ぜひ最後まで読んでみてください。
行列とは
行列とは数字を長方形でまとめた集合体のことをいいます。
具体的には次のようなものです。
$$ \begin{bmatrix}
4 & 1 & 7 \\
2 & 9 & 3 \
\end{bmatrix} $$
ここで、4、1、2など行列の内部にある数字を成分といいます。また、横を行、縦を列といいます。
例えば上の行列を行で見ると、4、1、7を1行目、2、9、3を2行目になります。一方で、列で見ると4と2は1列目、1と9は2列目、7と3は3列目です。
なので、この行列は2つの行と3つの列で表現されるので2×3行列、または(2,3)型行列といいます。
行列の種類
行列の種類は次のようなものがあります。
n次正方行列
n次正方行列とは行の数と列の数が同じ行列のことをいいます。ようは正方形の概形をしていて、次のように書けます。
$$ \begin{bmatrix}
1 & 2 \\
3 & 1 \
\end{bmatrix} $$
こちらは行と列が2つずつなので、2次正方行列です。
対角行列
対角行列とは対角線上にある成分以外0の行列のことです。
次のように書けます。
$$ \begin{bmatrix}
1 & 0 \\
0 & 2 \
\end{bmatrix} $$
単位行列
単位行列とは対角行列の特別なバージョンで対角線上の数が1の行列です。
次のように書けます。
$$ \begin{bmatrix}
1 & 0 \\
0 & 1 \
\end{bmatrix} $$
まとめ
本記事のポイントを以下にまとめます。
・行列とは数字を長方形でまとめた集合体
・行と列で構成されている
・種類としてn次正方行列、対角行列、単位行列がある
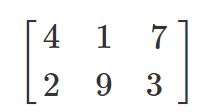

コメント