本記事では基本情報技術者試験にも出題されるオーダについて解説しています。目次は以下の通りです。
オーダとは
オーダを一言でいうとアルゴリズムの計算量のことを指します。
データ量が少ないとアルゴリズムの実行時間はさほど変わりませんが、データ量が多くなるとアルゴリズムの実行時間は変わっていきます。ただ、データ量の増加量とアルゴリズムの実行時間の増加量は同じとは限りません。
例えばデータ量が10倍に増えれば、実行時間も10倍になるアルゴリズムもあれば、実行時間が1倍のもあります。逆に実行時間が100倍になってしまうこともあります。
このようにオーダを知ることでアルゴリズムの実行時間の目安を知ることができます。
オーダ記法
オーダはO( )で表すことができます。( )の中身はnの関数で表すことができます。nの数字とオーダの関係の表を下に示します。
| オーダ | データ量と実行の時間との関係 | nを10倍したときの実行時間の増加量 | |
| 1 | \(O(1)\) | nの値と関係なく一定 | 1 |
| n | \(O(n)\) | 比例 | 10 |
| n² | \(O(n^2)\) | 2乗に比例 | 100 |
余談ですが、ループが1つあると\(O(n)\)、ループの中にループ(2重ループ)があると\(O(n^2)\)になります。
また、計算量の大小関係は\(O(1)<O(\log(n))<O(n^{1.25})<O(n\log_2(n))<O(n^2)<O(2^n)<O(n!) \)となります。
各アルゴリズムのオーダ
各アルゴリズムとオーダの関係を下の表に示します。
| アルゴリズム | オーダ |
| 基本交換法 | \(O(n^2)\) |
| 基本選択法 | \(O(n^2)\) |
| 基本挿入法 | \(O(n^2)\) |
| 線形探索法 | \(O(n)\) |
| 2分探索法 | \(O(\log_2(n))\) |
| ハッシュ探索法 | \(O(1)\) |
| ヒープソート | \(O(n\log_2(n))\) |
| シェルソート※1 | \(O(n^{1.25})\) |
※1計算量が変化するが大体この値になります。
まとめ
本記事のポイントを以下にまとめます。
・オーダとはアルゴリズムの計算量
・データ量の増え方と実行時間の増え方が同じであるとは限らない
・オーダはO( )で表す
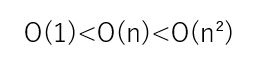

コメント