本記事では基本情報技術者にも出題される丸め誤差と打切り誤差について解説しています。
目次は以下の通りです。
演算誤差
演算誤差は、計算過程で発生する誤差のことで、数値計算において正確な結果を得るために考慮する必要がある要因です。
演算誤差の種類は以下のようなものがあります。
・桁落ち
・情報落ち
・丸め誤差
・打切り誤差
・オーバーフロー
・アンダフロー
本記事では丸め誤差と打切り誤差について説明しています。
丸め誤差
丸め誤差は有限のビット数で実数を表現し四捨五入などにより生じる誤差です。
例えば、0.01010101010101….は無限に出てくるので、どこかのタイミングで四捨五入なり切り捨てなりしないといけないですよね。
このように無限に続く実数を有限の桁数で表現すると、一部の実数は正確に表現できず計算結果に誤差が生じます。丸め誤差は四捨五入や切り捨てなどの演算によって発生し、計算結果が理論値からわずかにずれる現象です。
打切り誤差
打切り誤差は、有限桁の実数を無限に変換する際の計算途中での誤差です。
例えば1÷3をすると0.3333のようになり、循環小数になります。そうすると、どこかのタイミングで四捨五入なり切り捨てなりしないと
いけないですよね。
このように計算結果を有限桁で表現すると元の実数との差異が生じ、
誤差が発生します。この際計算の途中で生じた桁を切り捨てるか、
四捨五入などの方法で処理することがあります。
丸め誤差と打切り誤差の違い
ここで気になるところがこの二つの違いです。基本は両方とも無限に続く数字を処理にすることに誤差が生じているという共通点はありますが、違いを一言でいうと、「計算しているかしていないか」で問題ないです。丸め誤差の場合は計算していないときの誤差で、打切り誤差は計算しているときの誤差になります。
まとめ
本記事のポイントを以下にまとめます。
・演算誤差は、計算過程で発生する誤差
・丸め誤差は有限のビット数で実数を表現し四捨五入などにより生じる誤差
・打切り誤差は、有限桁の実数を無限に変換する際の計算途中での誤差
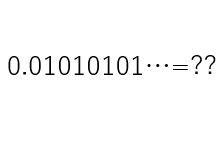

コメント