【機械学習】単回帰分析と重回帰分析について学ぼう

本記事では単回帰分析と重回帰分析について解説しています。
目次は以下の通りです。

線形回帰

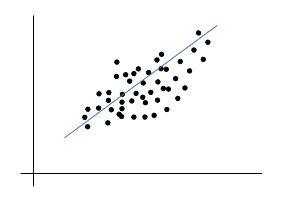
線形回帰は、機械学習の手法の一つで、2つ以上の変数間の関係をモデル化するために使用されます。
具体的には、線形回帰は一つ以上の説明変数と目的変数との間の線形な関係を推定する方法です。この関係を表現するために、回帰係数を用いて予測モデルを構築し、説明変数から目的変数の値を予測します。線形回帰は、実数値の目的変数を予測するために広く使用され、
教育、経済、科学などのさまざまな分野で応用されています。

単回帰分析

単回帰分析は、1つの説明変数を用いて線形回帰を行う統計的手法であり、簡単でシンプルな因果関係の解明に適した方法です。
単回帰分析の線形式は次の通りです。

$$ y=ax+b $$

ただし、aとb回帰係数、xは説明変数、yは目的変数です。

重回帰分析

重回帰分析は、複数の説明変数を用いて線形回帰を行う統計的手法であり、複数の要素が1つの目的変数にどのように影響するかを検証する際に使用される方法です。
重回帰分析の回帰式は次の通りです。

$$ y=a_1x_1+a_2x_2+・・・+a_n+x_n+b $$

ただし、a₁,a₂,a₃,…とb回帰係数、x₁,x₂,x₃,…は説明変数、yは目的変数です。

まとめ

本記事のポイントを以下にまとめます。