【機械学習】主成分分析について学ぼう！

本記事では主成分分析について説明しています。
目次は以下の通りです。

主成分分析とは？

主成分分析はPCAと呼ばれ、多くの変数を持つデータを集約し、主成分を作成する統計的な分析手法であり、次元削減の代表的な例です。PCAは教師あり学習ではなく、教師なし学習の一つです。

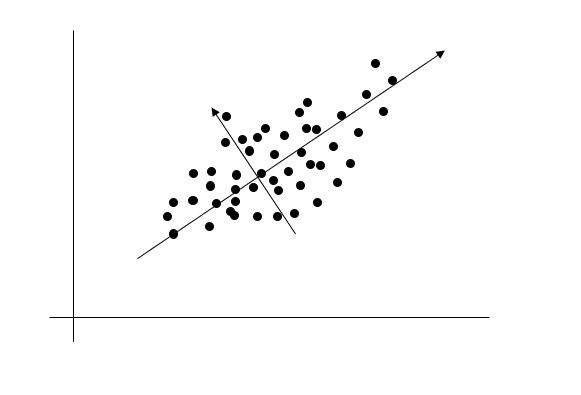
上の図のように2方向の矢印で分類できました。このようにデータのばらつきが大きい矢印が第1主成分となります。

主成分分析のメリットは、データの可視化のしやすさや情報の集約と変数の削減ができることです。しかしデメリットとしては、主成分の解釈が難しく元の変数の物理的な意味が失われる可能性があります。

そもそも次元削減とは？

次元削減は教師なし学習の一つでデータの特徴を保持しながら情報を抽出し、データを簡素化する学習手法です。

主成分分析のアルゴリズム

PCAのアルゴリズムは、以下のステップで説明できます。

1.データの中心化: 最初に元のデータセットから平均値を引いて、データを中心化します。
2.分散共分散行列の計算: 中心化されたデータから、各変数間の共分散を表す分散共分散行列を計算します。これはデータの特性を捉えるための基盤です。
3.固有値と固有ベクトルの計算: 分散共分散行列から、固有値とそれに対応する固有ベクトルを取得します。固有ベクトルは主成分を表し、固有値はその主成分がデータの分散をどれだけ説明するかを示します。
4.主成分の選択: 固有値の大きさに基づいて、主成分を選択します。
固有値が大きい成分から第1主成分、第2主成分として並べられます。
5.寄与率の計算: 各主成分の固有値を全固有値の合計で割り、それを寄与率として表現します。
寄与率は主成分がデータの分散をどれだけ説明するかを示す指標です。

まとめ

本記事のポイントを以下にまとめます。