本記事ではランレングス符号化とハフマン符号化について解説しています。目次は以下の通りです。
符号化の種類
符号化の種類は2種類ある
・通信している途中で起きた誤りを検出・訂正する作業を受信者が行える符号化
・送信する情報を短くすることで通信効率を高める符号化
本記事では後者の代表例であるランレングス符号化とハフマン符号化について扱います。
ランレングス符号化とは?
ランレングス符号化とは繰り返し回数と文字の組み合わせに置き換えることで圧縮を効率よく行う方法です。
以下の例をランレングス符号化します。
AAAABBBBB
このようにAが4回、Bが5回現れているので、4A5Bとなります。つまり、AAAABBBBB→4A5Bということになり、かなり圧縮できたことがお分かりになるかと思います。
ただ、繰り返し回数が1,2回だとその恩恵が少ないので、繰り返し回数が多ければ多いほど効果は絶大ということです。
ハフマン符号化とは?
ハフマン符号化とは出現確率が高いデータには短い符号、低いデータには長い符号を与えることで圧縮を効率よく行う方法です。
BACBAABACの例で考えます。
普通にやるとAが00,Bが01,Cが10なので、
0100100000010010になり、18ビットの長さになります。
これをハフマン符号化を用いて行います。
出現回数を見ると、Aが4回、Bが3回、Cが2回となります。
次に出現回数順に左から並べます。

つづいて以下のツリーみたいなものを書きます。
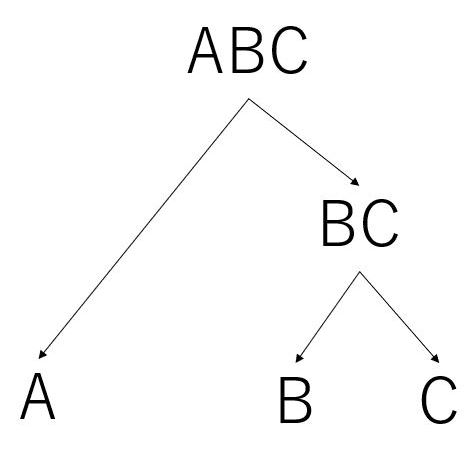
左に行くのを0,右に行くのを1とすると
ABCからAにいくには0
ABCからBにいくには10
ABCからCにいくには11
となります。ゆえに
BACBAABAC→10011100010011
となり、14ビットの長さになりました。
まとめ
本記事ではランレングス符号化とハフマン符号化について説明しました。
ランレングス符号化は、データの中で同じ文字や値が連続して現れる場合、その繰り返し回数と文字の組み合わせに置き換える手法です。一方、ハフマン符号化は、データの出現確率に基づいて、高確率のデータには短い符号語を、低確率のデータには長い符号語を与える方法です。


コメント